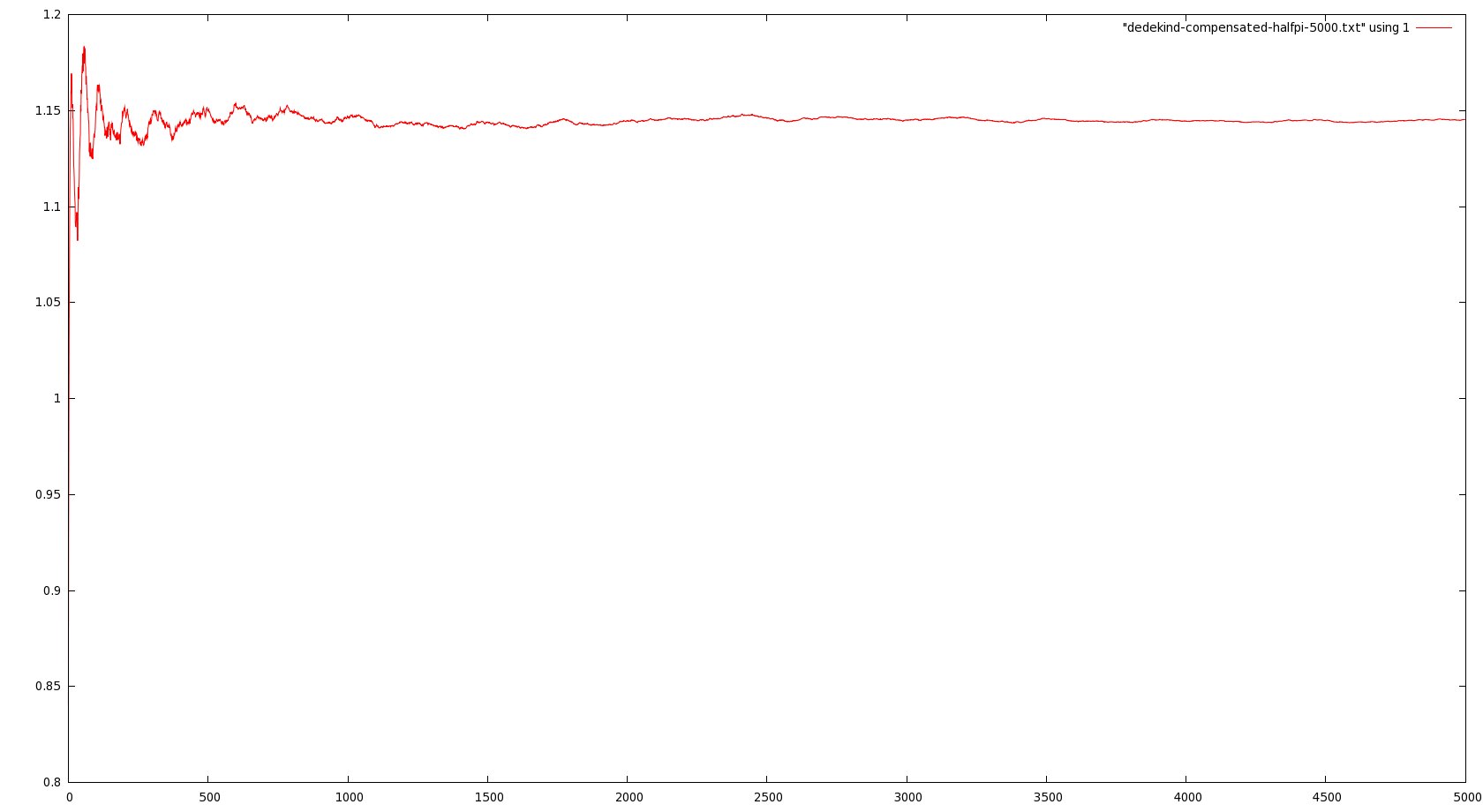
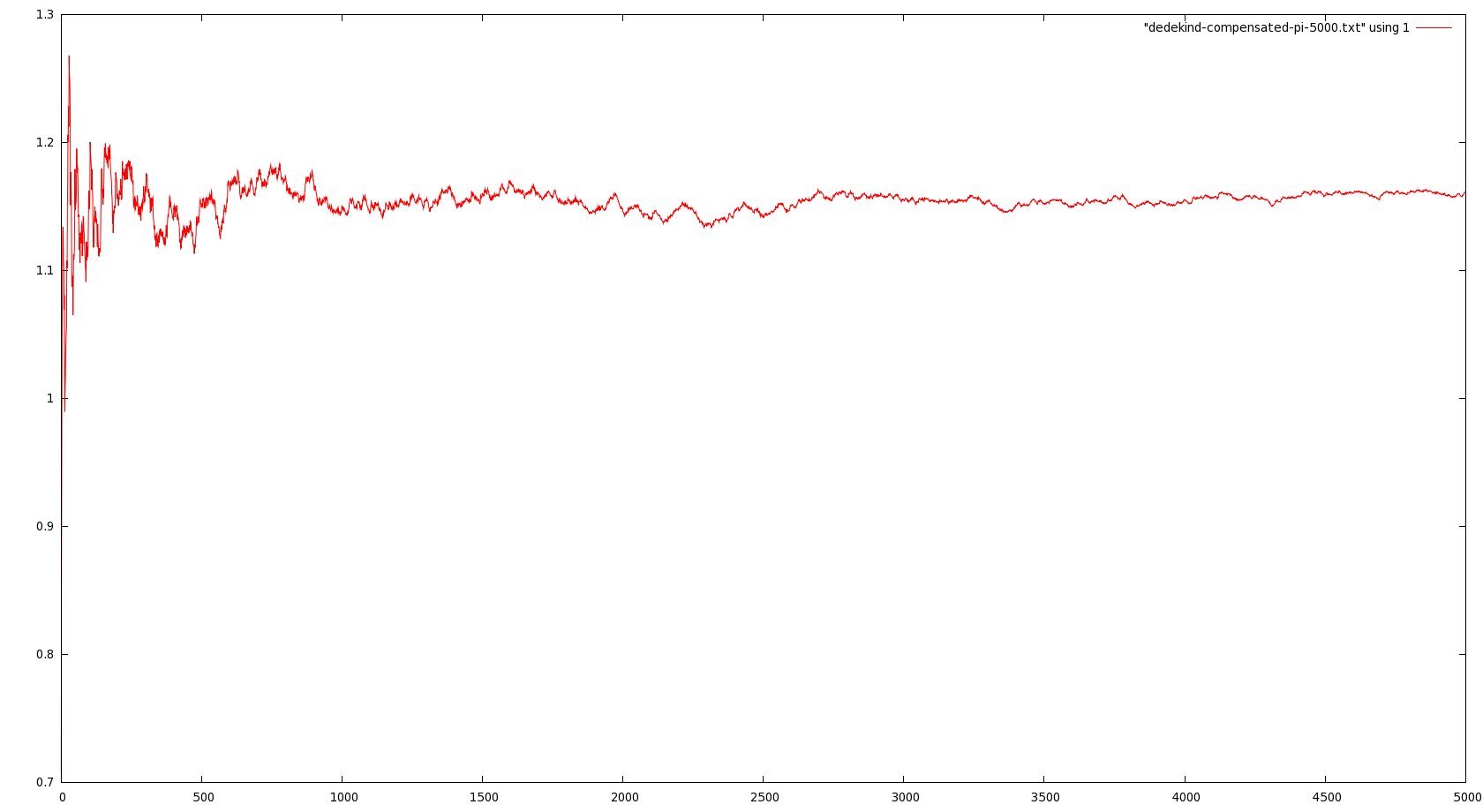
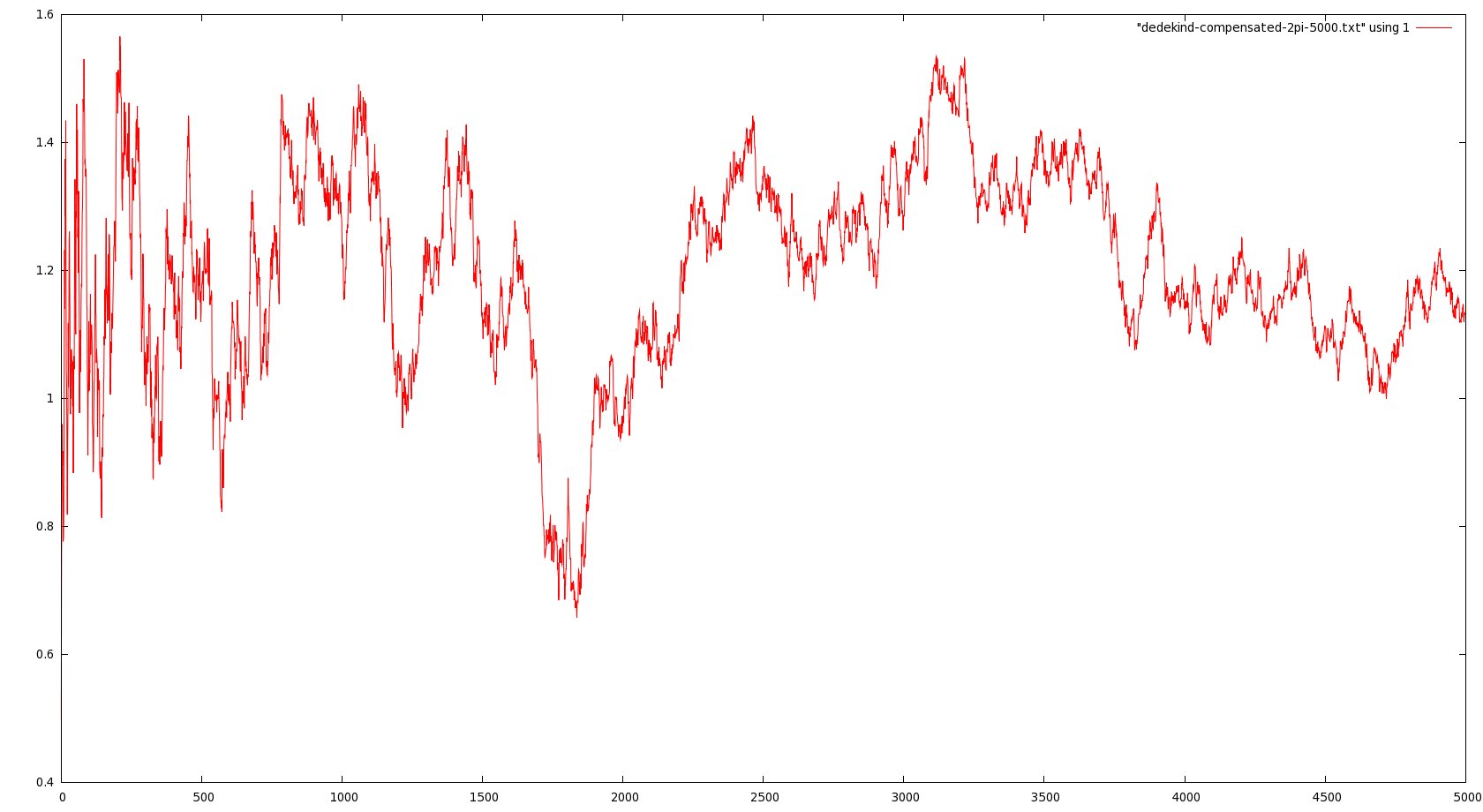
Here is a quick update to the last post about (restricted) mod-Cauchy convergence; I’ve investigated numerically the behavior of the renormalized averages
$latex \mathbf{E}_N(e^{its(d,c)}) \times \exp(\gamma_N |t|)$
(see the post for the notation) for some values of t, to see if the limitation to
$latex |t|<2\pi$
in Vardi’s result could be a mere artifact of the method. Here are some graphs representing these empirical averages for
$latex N\leq 5000$
(click to see the full pictures):
$latex t=\frac{\pi}{2}$
$latex t=\pi$
$latex t=2\pi$
$latex t=4\pi$
In particular, note that in the last picture, the vertical scale runs from -300 to 300, more or less, compared with oscillations between 0.5 and 1.5 in the third. So it seems pretty convincing evidence that the limit as N goes to infinity does not exist when t is large.
(Note: the empirical average for N=5000 involves about 8,000,000 Dedekind sums).